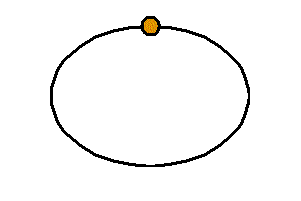
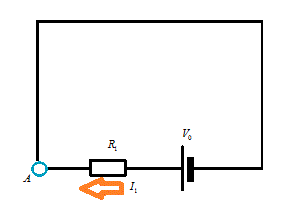
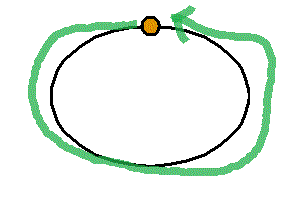
頂点数a=1 , 辺数b=1 , 1次元ベッチ数p1=1-a+b=1
- 未知数I1
- キルヒホッフ第1法則 0
- キルヒホッフ第2法則 1
- 「枝分かれポイント」はないから、キルヒホッフ第1法則を用いる場面がない。
キルヒホッフ第1法則の式の数は、a-1かも知れない。
- 「閉回路」は1個だけあって、ここにキルヒホッフ第2法則を適用し、未知数1個の値が計算される。
未知数の個数は、b、
キルヒホッフ第2法則の式の数は、p1かも知れない。
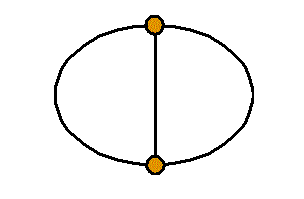
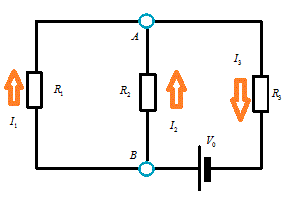
頂点数a=2 , 辺数b=3 , 1次元ベッチ数p1=1-a+b=2
- 未知数I1 , I2 , I3
- キルヒホッフ第1法則 1
- A: +I1+I2-I3=0・・・(1*1)
- B: -I1-I2+I3=0・・・(1*2)
-(1*2)=(1*1)
- キルヒホッフ第2法則 1
- +R1I1-R2I2=0・・・(2*1)
- +R2I2-V0+R3I3=0・・・(2*2)
- +R1I1-V0+R3I3=0・・・(2*3)
(2*1)+(2*2)=(2*3)
- 「枝分かれポイント」が2ヵ所あるから、キルヒホッフ第1法則の式は2個現れる。しかし2式は同値であるから、独立なものは1個である。
やはり、キルヒホッフ第1法則の式の数は、a-1かも知れない。
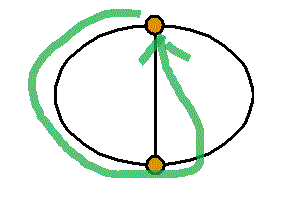
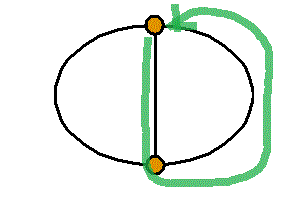
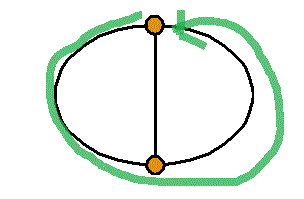
- 「閉回路」は3個あり、キルヒホッフ第2法則の式は3個成立する。しかしこれらのうちいずれか2式から残りの式を導くことができるから、独立なものは2個である。
やはり、キルヒホッフ第2法則の式の数は、p1かも知れない。
未知数の個数は、b、とすると、独立な条件式の個数が、(a-1)+p1=b、となり、辻褄が合っている!
では、「閉回路」の個数3はどう表されるのだろう?
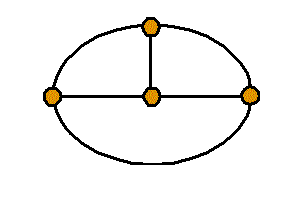
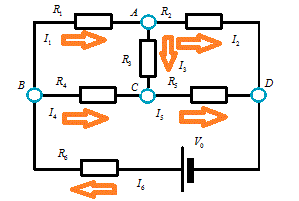
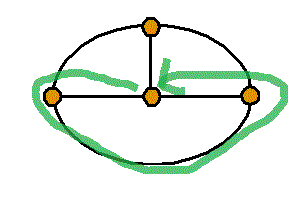
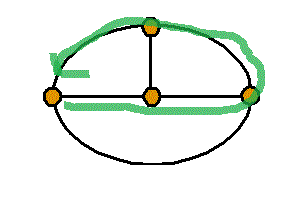
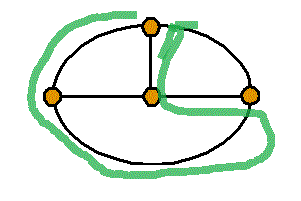
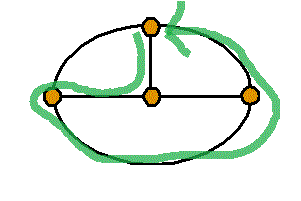
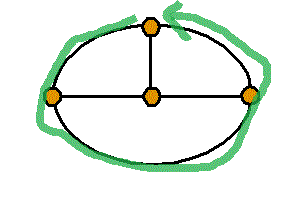
頂点数a=4 , 辺数b=6 , 1次元ベッチ数p1=1-a+b=3
- 未知数I1 , I2 , I3 , I4 , I5 , I6
- キルヒホッフ第1法則 3
- A: +I1-I2-I3=0・・・(1*1)
- B: -I1-I4+I6=0・・・(1*2)
- C: +I3+I4-I5=0・・・(1*3)
- D: +I2+I5-I6=0・・・(1*4)
(1*1)+(1*2)+(1*3)=-(1*4)
- キルヒホッフ第2法則 1
- +R1I1-R4I4+R3I3=0・・・(2*1)
- -R3I3-R5I5+R2I2=0・・・(2*2)
- +R4I4+R6I6-V0+R5I5=0・・・(2*3)
- -R4I4-R5I5+R2I2+R1I1=0・・・(2*4)
- +R1I1+R6I6-V0+R5I5+R3I3=0・・・(2*5)
- -R3I3+R4I4+R6I6-V0+R2I2=0・・・(2*6)
- +R1I1+R6I6-V0+R2I2=0・・・(2*7)
(2*1)+(2*2)=(2*4)
(2*1)+(2*3)=(2*5)
(2*2)+(2*3)=(2*6)
(2*1)+(2*2)+(2*3)=(2*7)
- 「枝分かれポイント」は4ヵ所あるが、独立なキルヒホッフ第1法則の式は、3個、a-1に合致する!
- 「閉回路」は
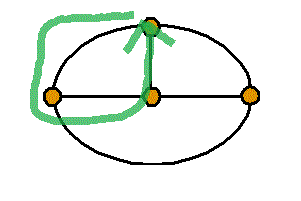
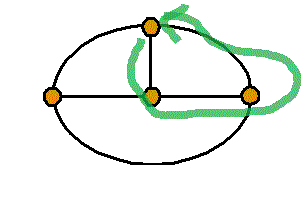
線で囲まれた1区画のみのまわりを廻るもの、3個、
2区画のまわりを廻るもの、3個、
3区画のまわりを廻るもの、1個、合計7個。
キルヒホッフ第2法則の式は、7個現れるが、このうちの3個で他の4個を導けるから、独立なものは3個、これもp1に合致する!
しかし、「閉回路」の個数7がどう導かれるかは、依然、謎である。
ここまでの「予想」。
- 未知数の個数は、辺数bに等しい。
- 独立なキルヒホッフ第1法則の式の数は、頂点数から1を引いたもの、a-1に等しい。
- 独立なキルヒホッフ第2法則の式の数は、未知数の個数bから独立なキルヒホッフ第1法則の式の数a-1を引いたもの、b-a+1、すなわち、1次元ベッチ数に等しい。
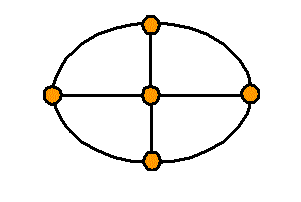
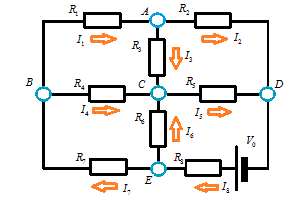
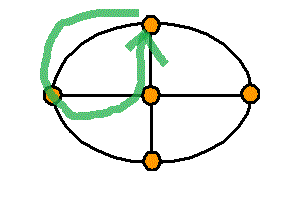
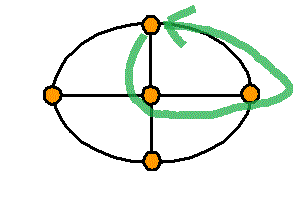
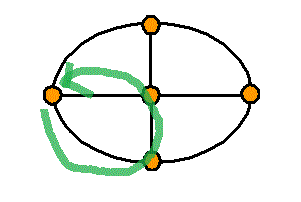
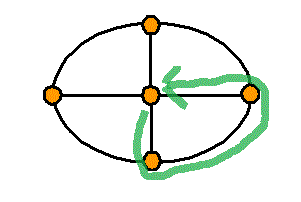
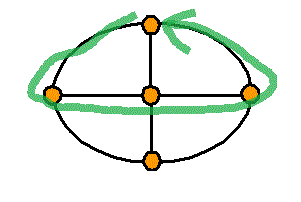

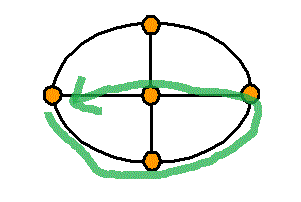
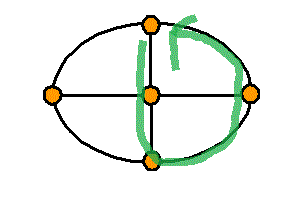
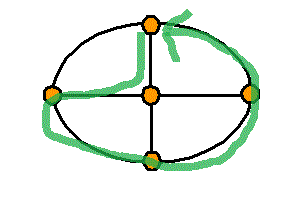
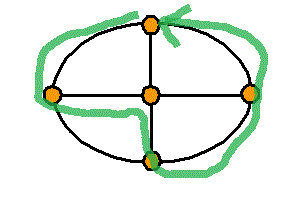
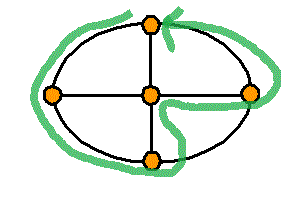
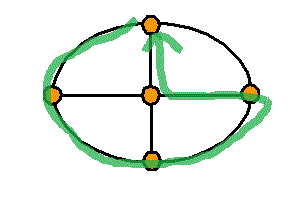
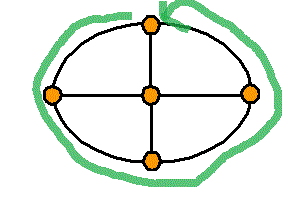
頂点数a=5 , 辺数b=8 , 1次元ベッチ数p1=1-a+b=4
- 未知数I1 , I2 , I3 , I4 , I5 , I6 , I7 , I8
- キルヒホッフ第1法則 a-1=4
- キルヒホッフ第2法則 p1=1-a+b=4
これで解けるはずである。もう、やらないけど(笑)。
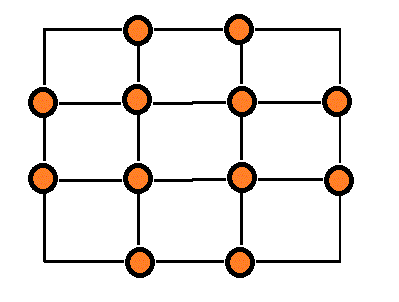
頂点数a=12 , 辺数b=20 , 1次元ベッチ数p1=1-a+b=9
- 未知数I1 ~ I20
- キルヒホッフ第1法則 a-1=11
- キルヒホッフ第2法則 p1=1-a+b=9
戻る/次
































